Guia Completo para Regressão Linear Simples com Python

Se você está explorando regressão linear, seja para estudos de econometria ou aplicações práticas, entender o código em Python que cria uma regressão linear simples é essencial. Aqui, vamos destrinchar o código passo a passo e mostrar como ele se aplica para visualização e análise. Vamos mergulhar nessa jornada usando bibliotecas populares como numpy, matplotlib e scipy.

---

O que é Regressão Linear Simples?

A regressão linear simples é uma técnica estatística usada para modelar a relação entre duas variáveis. A fórmula básica é:

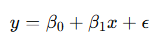
• y: Variável dependente (o que queremos prever)
• x: Variável independente (o fator que influencia y)
• β0​: Intercepto
• β1​: Coeficiente angular (inclinação)
• ϵ: Erro aleatório

Agora que sabemos o que estamos construindo, vamos ao código!

Como Fazer uma Regressão Linear Simples em Python

---

Importando Bibliotecas Essenciais

O primeiro passo é importar as bibliotecas necessárias:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

• numpy: Para trabalhar com arrays e gerar dados.
• matplotlib: Para criar gráficos e visualizar resultados.
• scipy.stats: Para realizar cálculos estatísticos, como regressão linear.

---

Gerando Dados para a Regressão

Antes de aplicar a regressão linear, precisamos de um conjunto de dados:

np.random.seed(0)  # Garante reprodutibilidade
x = np.linspace(0, 10, 100)  # Gera 100 valores espaçados entre 0 e 10
y = 2 * x + 1 + np.random.normal(0, 1, x.shape)  # Gera y com ruído

O que está acontecendo?

1. np.linspace cria valores igualmente espaçados para xxx.
2. A fórmula y = 2 * x + 1 define uma relação linear com inclinação 2 e intercepto 1.
3. Adicionamos ruído aleatório com np.random.normal para simular variabilidade real nos dados.

---

Aplicando a Regressão Linear

Agora que temos os dados, ajustamos o modelo de regressão linear:

pythonCopiar códigobeta1, beta0, r_value, p_value, std_err = stats.linregress(x, y)

• beta1: Inclinação (β1​).
• beta0: Intercepto (β0​).
• r_value: Coeficiente de correlação (r), indicando a força da relação.
• p_value: Probabilidade associada ao teste de hipótese (p).
• std_err: Erro padrão da inclinação.

---

Visualizando os Resultados

A visualização ajuda a interpretar o modelo:

plt.scatter(x, y, label='Dados')  # Gráfico de dispersão dos dados
plt.plot(x, beta0 + beta1 * x, color='red', label=f'Regressão Linear')  # Linha de regressão

# Adicionando a equação e o coeficiente de correlação no gráfico
equation_text = f'y = {beta0:.2f} + {beta1:.2f}x'
r_text = f'r = {r_value:.2f}'
plt.text(1, 18, equation_text, fontsize=12, color='red')
plt.text(1, 16, r_text, fontsize=12, color='blue')

# Personalizando o gráfico
plt.title("Regressão Linear Simples com Equação")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()

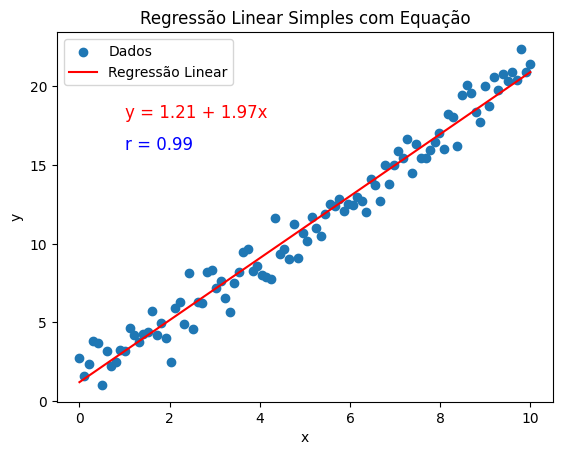
O que está sendo exibido?

1. Dados: Gráfico de dispersão para mostrar a variabilidade.
2. Linha de Regressão: Representa a melhor aproximação linear para os dados.
3. Equação: Mostra a fórmula ajustada y=β0+β1x.
4. Correlação (r): Mostra a força da relação entre x e y.

---

Interpretação dos Resultados

1. Inclinação (β1​): Mostra quanto y muda para cada unidade de x.
2. Intercepto (β0​): Valor de y quando x=0.
3. Coeficiente de Correlação (r):
   • r=1: Relação linear perfeita positiva.
   • r=0: Nenhuma relação linear.
   • r=−1: Relação linear perfeita negativa.

Análise Gráfica

E você? Sabe fazer as suas regressões?